The Greenberg-Hastings
Cellular Automaton
by Tom Bohman and Janko Gravner
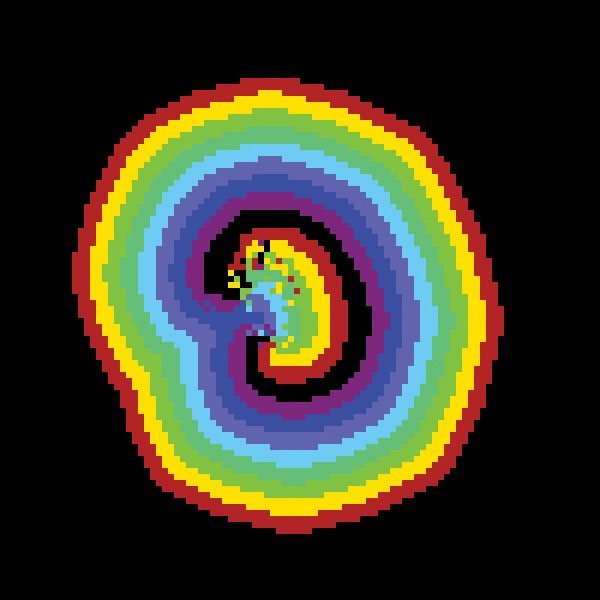
The image on the cover was generated by the Greenberg-Hastings model. This cellular automaton was introduced by Jim Greenberg and Stuart Hastings as a simple discrete model that generates the complex spatial patterns observed in excitable media such as nerve tissue and the Belousov Zhabotinsky chemical reaction. These patterns are generally spontaneous, self-exciting, spatially homogeneous oscillations. The fact that this simple model generates such striking complexity inspired interest in cellular automata as models of complex systems. We placed this image on the cover in honor of Jim Greenberg.
The classical Greenberg-Hastings model evolves in discrete time on the 2-dimensional integer lattice. The model has three parameters: a finite set \(N\) \(⊂\) \(Z\)\(^2\), which defines the neighborhood of the origin, a positive integer \(k\), which is the refractory period for the model, and a positive
integer \(t\), which is the excitation threshold.
The state space for the model is
\(\left\{ 0, 1, … , k + 1\right\}\) and the neighborhood of a site \(x ∈ Z^2\) is \(x + N\). State \(0\) is the resting state, state \(1\) is the excited state, and states \(2, … , k + 1\) are the refractory states. We begin with an initial configuration,
\(f_0:Z^2\) \(\rightarrow\) \(\left\{0,1, … , k+1\right\}\)
Given the configuration \(f_i\) , the configuration \(f_{i +1}\) is determined for all points in the integer lattice simultaneously and in parallel. If \(x\) is excited or is in one of the first \(k –1\) refractory states then \(x\) proceeds to the next refractory state; to be precise, if \(f_i\) \(\left(x\right)\) \(∈\) \(\left\{1, … , k \right\}\) then
\(f_{i +1}\) \(\left(x\right)\) \(= f_i\) \(\left(x\right)\) \(+ 1\). If \(x\) is in the last refractory state at time \(i\) then it is in the resting state at time \(i + 1\); that is, if \(f_i\) \(\left(x\right)\) \(= k +1\) then \(f_{i +1}\) \(\left(x\right)\) \(= 0\). A position \(x\) that is resting becomes excited if a sufficient number of its neighbors are excited.
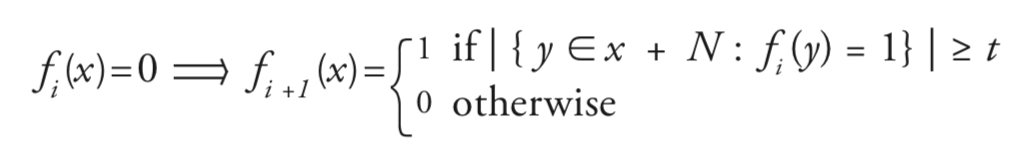
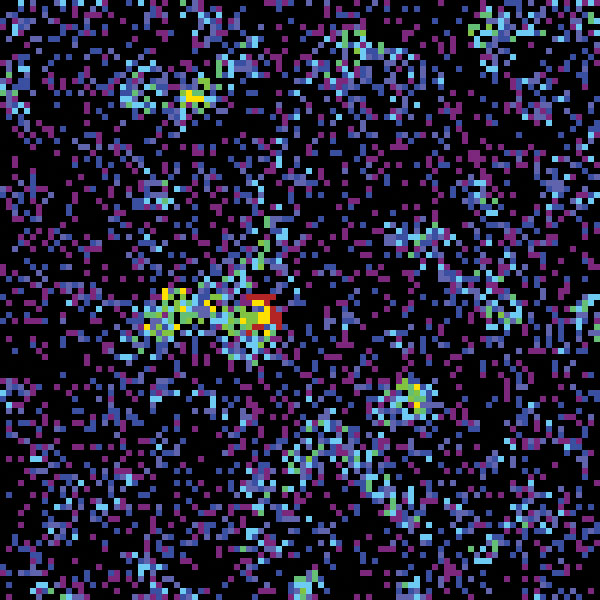
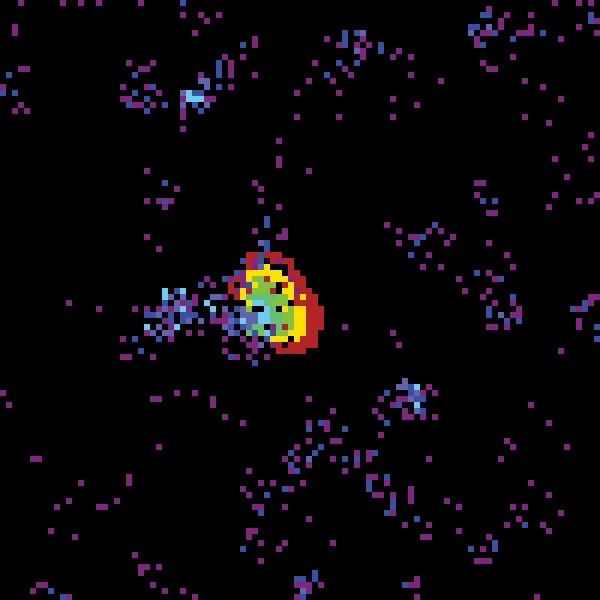
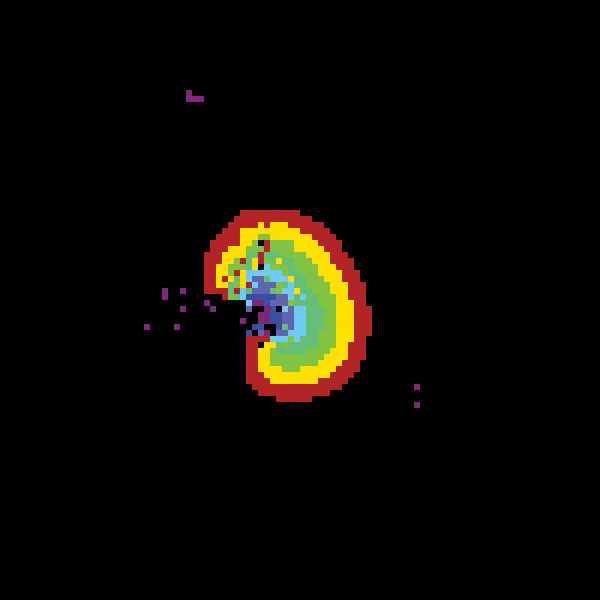
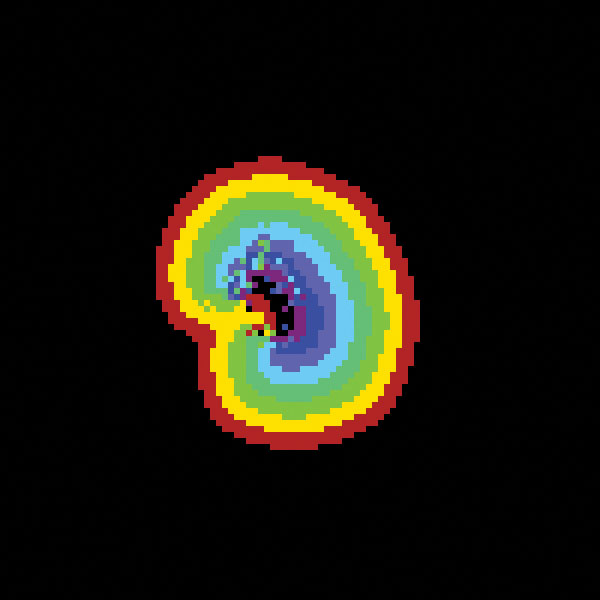
The sequence of images depicted above are generated by Greenberg-Hastings using the following parameters. The neighborhood is a range three box (i.e., the neighborhood of a point x is the set of 49 points of \(l∞\) distance at most 3 from \(x\)), the excitation threshold is \(t = 5\), and there are 9 states (so there are \(k = 7\) refractory states). This sequence begins with a random configuration and shows how local stationary periodic configurations spontaneously emerge and generate waves in the dynamics.
| black | state 0 | resting state |
| orange | state 1 | excited state |
| yellow | state 2 | refractory state |
| light green | state 3 | refractory state |
| aqua | state 4 | refractory state |
| light blue | state 5 | refractory states |
| lavendar | state 6 | refractory state |
| dark blue | state 7 | refractory state |
| purple | state 8 | refractory state |
(We also use colors to indicate the states in the image on the cover, but in a slightly different way. Black again indicates the resting state. The orange squares are again the excited states — these are raised on the cover. The refractory states are in successively darker shades as the refractory states progress toward the resting state.)
References
Robert Fisch, Janko Gravner, and David Grieath, Metastability in the Greenberg-Hastings model. Ann. Appl. Probab. 3 (1993), 935-967.
Janko Gravner, Hanbaek Lyu and David Sivako, Limiting behavior of 3-color excitable media on arbitrary graphs, Ann. Appl. Probab. 28 (2018), 3324-3357.
James Greenberg and Stuart Hastings, Spatial patterns for discrete models of diffusion in excitable media. SIAM J. Appl. Math. 34 (1978) 515-523.