Frick’s Fellowship
Assistant Professor Florian Frick was among 126 recipients of 2019 Sloan Research Fellowships, which honor early career scholars.
“Sloan Research Fellows are the best young scientists working today,” said Adam F. Falk, president of the Alfred P. Sloan Foundation in announcing the 2019 fellowships. “Sloan fellows stand out for their creativity, for their hard work, for the importance of the issues they tackle and the energy and innovation with which they tackle them. To be a Sloan fellow is to be in the vanguard of 21st century science.”
The Sloan Fellowships are open to scholars in eight scientific and technical fields — chemistry, computer science, economics, mathematics, computational and evolutionary molecular biology, neuroscience, ocean sciences and physics. Winners receive a two-year, $70,000 fellowship to further their research ideas and further their work on common projects.
For Frick, who has collaborators scattered around the United States and Europe, the fellowship will allow him to invite them to Carnegie Mellon to develop new ideas and further their work on common projects.
“Over the next two years, I hope to expand the reach of topological methods and find numerous new problem areas that can benefit from a topological viewpoint,” Frick said of his plans for the fellowship. He noted that these geometric and topological methods can yield fruitful results in other branches of mathematics and their applications.
Frick describes his research as working “at the triple-point of combinatorics, topology and geometry.” An example of Frick’s research is his work to determine whether it’s possible to find four points that form a square within a curve in a plane. Another area of mathematics he’s interested in is one that has been relatable to many people at some point in their lives: fair rent division.
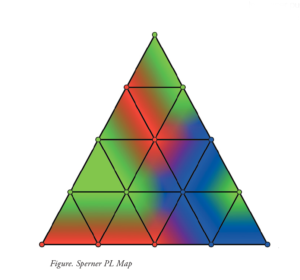
In a paper published this year in The American Mathematical Monthly, Frick and his collaborators introduced an algorithm based on Sperner’s lemma proving that one can achieve “rental harmony” even while only taking into consideration the preferences of two out of three of the roommates sharing an apartment.
Another study of Frick published this year in the Society for Industrial and Applied Mathematics Journal on Applied Algebra and Geometry found new obstructions for intersection patterns to arise from arrangements of convex open sets in Euclidean space. These obstructions completely classify intersection patterns for a more flexible topological relaxation of arrangements of convex open sets.
This question has applications to neuroscience, particularly for studying cofiring patterns of so-called “place cells” in the brain that fire when an organism is in a certain place in its environment.
A native of Germany, Frick came to Carnegie Mellon in 2018 from Cornell University, where he was a H.C. Wang assistant professor. During that time, he also spent a semester as a postdoctoral fellow at the Mathematical Sciences Research Institute in California. He earned his Ph.D. in 2015 from Technische Universität Berlin, from which he also obtained his bachelor’s and master’s degrees.
Avoiding Coincidences
Read Florian Frick’s latest paper in PDF format.