
One such application is numerical integration: given a function f, the aim is to compute the definite integral ∫\(_{[0,1]^d}\) f. If f has a nice antiderivative, we may compute the integral using the Fundamental Theorem of Calculus. Sadly, most functions have no nice antiderivatives and so one must resort to numerical approximations.
Consider the approximation of ∫\(_{[0,1]^d}\)f by a finite sum \(\frac {1}{n}\) ∑p∈P f(p), where P is an n-points set. What happens if P is the grid? The good news is that by the very definition of the Riemann integral, the sum converges to the integral as n → ∞. The bad news is that the convergence is quite slow even for very well-behaved functions.
For example, for the step function f(\(x_1, . . . , x_d)\)=1 \(_{x1\leq a}\) the approximation error is proportional to n−1/d for the most values of n. This is impractically large even for d = 5. One might be tempted to blame this on the discontinuity in f. However even for the function x12 the error is proportional to n−2/d.
It turns out that the grid points are a poor choice for our integration method because some axis-parallel boxes contain too few points, whereas others contain too many. Here, by axis-parallel box we mean a set of the form B=[\(a_1, b_1\)) × · · · × [ad,bd), and by too few and too many we mean that the number of points of P that are in B deviates significantly from n vol(B), which is the number of points that we expect to fall into B had it been completely uniformly distributed.
Discrepancy of a set B is the difference discP(B)=|P∩B|−n vol(B). Discrepancy of P is discP=max discP(B), where the maximum is over all axis-parallel boxes. For example, discrepancy of the regular grid is Θ(n1−1/s). Koksma and Hlawka showed that the approximation error for integration of functions of bounded variation is behaves like \(\frac {1}{n}\) disc P in the worst case. Intuitively, integration with respect to a high-discrepancy set assigns undue weight to some subregions of [0, 1]d at expense of the others.
It is a fascinating open problem to find sets of smallest discrepancy in \([0, 1]^d\). The best existent constructions have discrepancy of asymptotic order logd−1n in dimension d. One such construction is the Halton–Hammersley sets. It is easy to define these sets for d=2: given a natural number m whose base-2 expansion is at · · · a1a0, its reversal is the binary number r(m)=0.a0a1 · · · at.
Halton–Hammersley set is {(m/n, r(m)) : m=0, 1, . . . , n − 1}. The higher-dimensional Halton–Hammersley sets are defined similarly using digit reversals of m when written in several prime bases.
Planar Halton–Hammersley sets with n=2k points have a peculiar property: they have zero discrepancy on every axis-parallel rectangle of the form [a1 /2s , b1 /2s ) × [a2 /2t , b2 /2t ) with s + t ≤ k. In discrepancy theory, a set with this property is called a net.
In addition to their uses in numerical algorithms, nets are also useful in combinatorial geometry. One such application is to the problem of convex holes. A convex hole in a set P ⊂ ℝd is a subset H ⊂ P that are vertices of a convex polytope; it is called ℓ-hole if |H|=ℓ. Erdős asked if, for every fixed ℓ, all sufficiently large planar sets in general position contain an ℓ-hole. Horton answered Erdős’s question in negative: he constructed arbitrarily large planar sets without 7-holes. Valtr generalized Horton’s construction to higher dimensions; he showed that there exist arbitrary large sets in ℝd without f(d)-holes for some function f that is slightly larger than the factorial. Recently, in a collaboration with Professor Holzman from Haifa, graduate student Ting-Wei Chao and the author showed that the sets of Horton and Valtr are Halton–Hammersley sets in disguise.
To be precise, Horton’s set is obtained from the planar Halton–Hammersley by stretching y-coordinates; the y-coordinate 0.a0a1 · · · (in binary) becomes a0 Y0 + a1 Y1 + · · · where Y0 ≫ Y1 ≫ · · · is a quickly-decaying sequence of real numbers. A similar transformation turns any net into a set without large holes. Using this relation, new sets in ℝd without cd-holes were found. It is conjectured that the exponential bound is tight but the best lower bound for d ≥ 3 is mere 2d + 1.
■ Boris Bukh
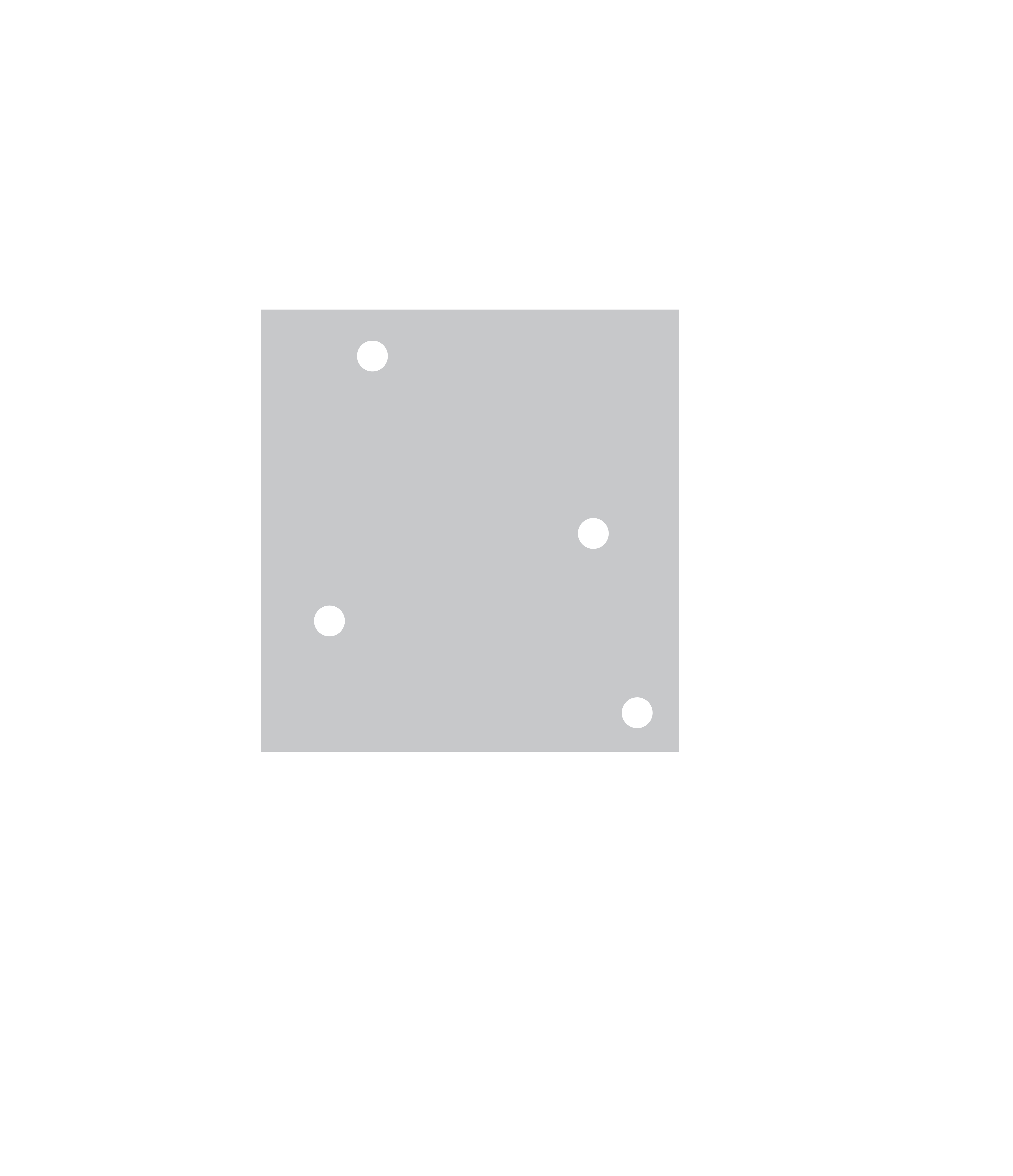
Figure 1: Discrepancy of a box is the difference between the expected and the actual number of points inside.
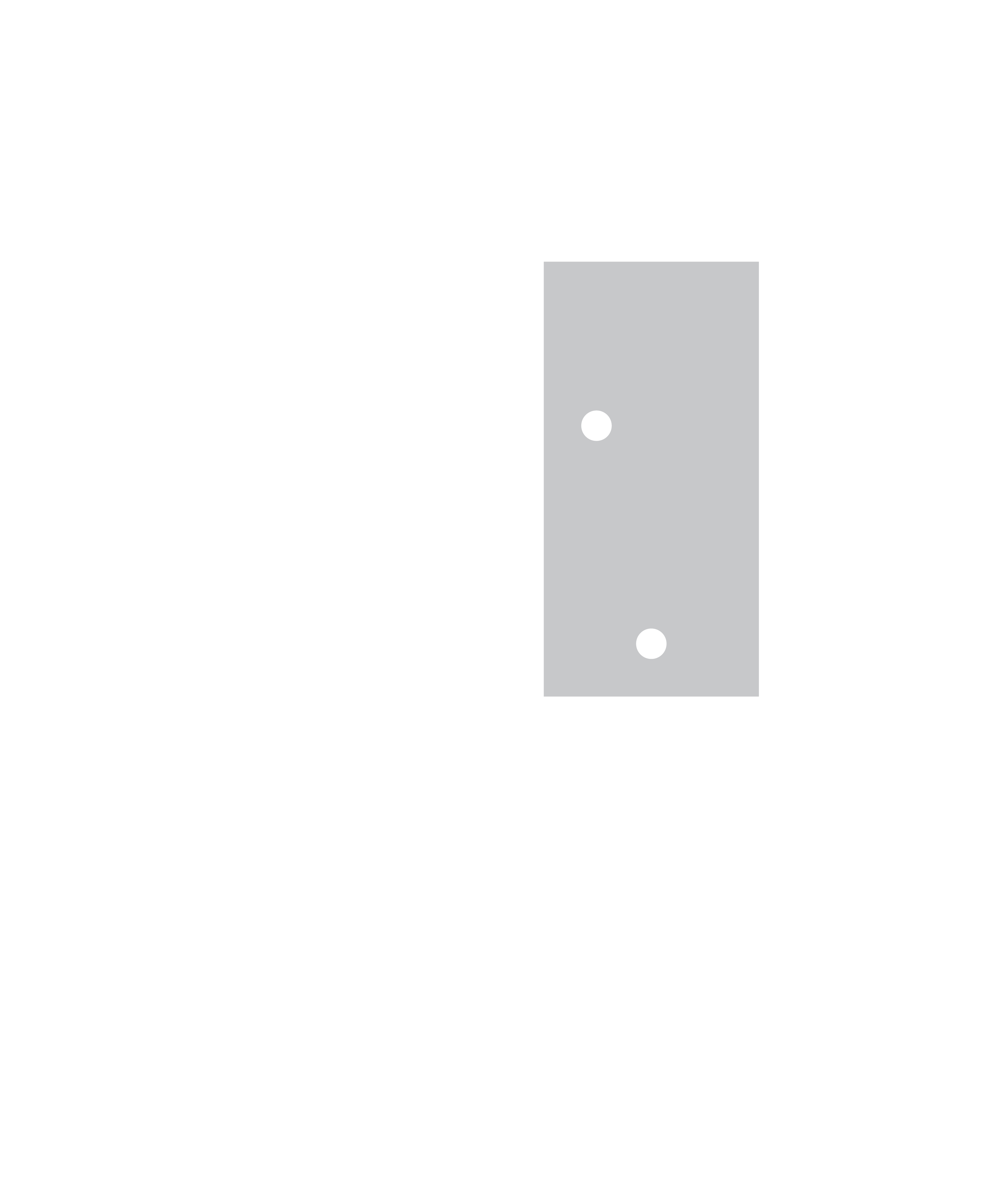
Figure 2: Halton-Hammersley set of size 16. The number of points in every not-too-small dyadic rectangle is exactly proportional to its area.
Figure 3: A 5-hole in a planar set.
