Volatility Surface

$Research roundup$

For their work on option pricing, Robert C. Merton and Myron Scholes won the 1997 Nobel Prize in Economics. Fischer Black, who joined Merton and Scholes in this work, died in 1995 and was therefore ineligible to share in the Nobel Prize. The results of Black, Merton and Scholes, and subsequent ideas developed to better understand and extend their results, have revolutionized the finance industry. This has made it possible to manufacture, price and manage a wide variety of financial products essential for smooth functioning of the global economy. It has also given rise to the field of quantitative finance.

To understand the beginning of quantitative finance, consider a European call option that confers the right to buy a share of stock $T$ years from now at a strike price $K$. Let $S(T)$ denote the (today unknown) price of a share of the stock $T$ years from now. The value $T$ years from now of the European call will be max{$S(T) − K, 0$}. To see this, consider the two cases $S(T) > K$ and $S(T) \leq K$. If $S(T) > K$, the owner of the option will exercise it and receive a share of stock valued at $S(T)$ in exchange for a payment $K$. Thus, if $S(T) > K$, the option will have value $S(T) − K$. On the other hand, if $S(T) \leq K$, the option to buy a share of the stock in exchange for a payment $K$ will be worthless.

But what is the price of the European call today (time 0) when we do not know what the stock price will be $T$ years from now (at time $T$)? According to the Black-Scholes option pricing formula, this is

$equation_01$

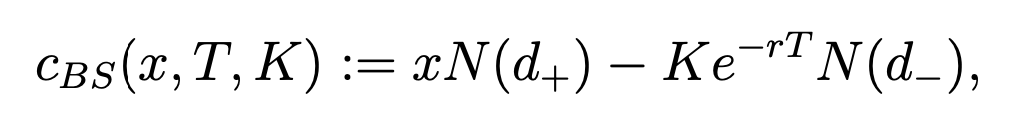
where

$equation_02$

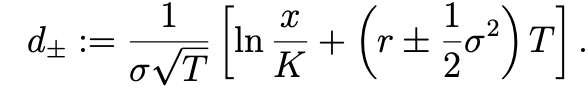
In this formula, $N$ is the standard normal cumulative distribution function, $x$ is the price of a share of the stock today, $r$ is an annual interest rate, and σ, a positive constant, is the volatility of the stock.

The model underlying this formula is that the stock price is a random process with dynamics

$equation_03$

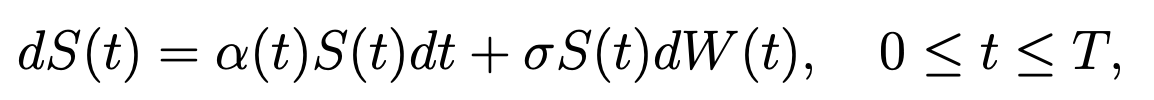
with $S(0) = x$. Here $W$ is a Brownian motion and $α(t)$, which can be random, is the “instantaneous” expected rate of return of the stock at time $t$.

The justification for the Black-Scholes formula is the following. If one begins at time 0 with capital $c_{BS} (x,T,K)$, it is possible to continuously trade in the stock and a money market account with interest rate r, without any additional infusion of capital, in order to create a portfolio whose value at time $T$ will be max${S(T)−K, 0}$ with probability 1. Because one can thereby “manufacture” the call payoff at time $T$ beginning with capital $c_{BS} (x,T,K)$ at time $0$, $c_{BS} (t,x,K)$ must be the price of the call at time $0$.

A consequence of the Black-Scholes formula is the surprising observation that the expected rate of return of the stock is irrelevant to the price of an option to buy the stock; the term $α(t)$ does not appear in the formula. Instead, the key parameter in the pricing formula is the stock volatility, which unlike the instantaneous expected rate of return, is assumed to be constant.

The Black-Scholes formula as written above provides the price of European calls, the right to buy a share of stock at a future date at a pre-specified price. In addition, it implies the prices of European puts, the right to sell a share of stock at a future date at a prespecified price. This is because of a model-independent relationship between European call and European put prices known as put-call parity.

From the time of the publication of the Black-Scholes formula in 1973 until the 1987 stock market crash, the formula proved to be remarkably consistent with market prices of options. After 1987, option prices on many underlying processes, most notably the S&P 500 index, are no longer consistent with the Black-Scholes formula with a constant volatility. Instead, they exhibit a “smile,” in which the volatilities that must be used in the formula to obtain the market prices of European put options with strike prices $K$ below the current stock price $x$ are higher than the volatilities needed to obtain the market prices of European call options with strike prices $K$ above the current stock price $x$.

Fortunately, the theory of quantitative finance has moved well beyond the restrictive assumptions behind the original Black-Scholes formula. There are many ways to generalize the dynamics of the underlying stock price and still obtain an option pricing formula. One of these generalization admits the possibility that the volatility is a function $σ(t, s)$ of time t and the underlying stock price $s$. This function, called the volatility surface, can be deduced from European call prices. Indeed, if we denote by $c_{Mkt}(x, T, K)$ the market price today of the option to buy a share of stock $T$ years from now at price $K$, then Dupire has shown that we should use in the stock price dynamics the time- and price-dependent volatility given by

$equation_04$

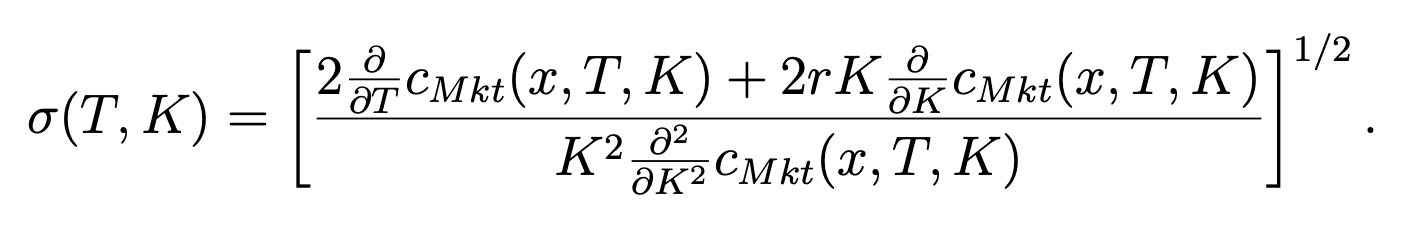
This formula for σ takes option prices as inputs. Because of the extensive market in options that has developed since the Black-Scholes formula was discovered, it is reasonable to assume that the right-hand side of Dupire’s formula can be computed from market data. This produces a function σ that can be used in the so-called local volatility model of the underlying stock price dynamics

$equation_05$

These dynamics can then be used to price “exotic” derivative securities, such as the option to buy a share of stock $T$ years from now at price $K$ unless the stock price rises above a level B between today and the option expiration at time $T$. An agent who does not want to pay the full price of a European call might be willing to purchase such a “knock-out” option because she or he is confident the stock price will not exceed $B$ before time $T$. A less exotic and quite common option that can also be priced using a local volatility model is an American put, which confers the right to sell at price $K$ a share of stock at any time prior to time $T$, not just at time $T$. Such a product provides insurance against major loss to agents holding the stock.

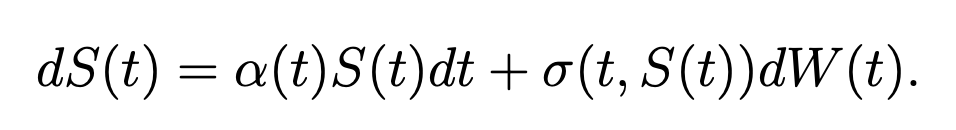
Options are an example of derivative securities, securities whose value is derived from some other underlying security or process. While the discussion above refers to options on stocks, the underlying process on which the option is written need not be a stock and in place of the option there might be a more complex derivative security. For example, the underlying process might be a variable interest rate, and the derivative security might be an interest rate cap on a variable rate mortgage. The underlying asset might be a bond, and the derivative security might be a credit default swap that insures the bond holder against bond default. There might be multiple underlying assets, currencies for instance, and the derivative security might be the option to swap a sequence of payments in one currency for a sequence of payments in a different currency. As mentioned at the outset, quantitative finance has made it possible to create and manage the risk associated with a wide variety of products, and these are critical to the functioning of the global economy.

■Steve Shreve

Staff News

Alumni News