Research Feature
The traveling salesperson problem:
an analysis of typical instances
By Alan Frieze
Research
Feature
1. Introduction
The Traveling Salesperson Problem (TSP) is arguably the most studied of all the hard combinatorial optimization problems. There are several books, [13], [20], thousands of papers and even a phone app. dedicated to the problem. It can be described as follows. There are \(n\) cities and the distance between city \(i\) and city \(j\) is \(C(i,j)\) for \(1\leq i,j\leq n\). A salesperson starts in city 1 and has to visit each of the other cities, once and only once in sequence \(\sigma=(1=i_1,i_2,\ldots,i_n)\) and then return to city 1. Such a sequence is called a tour. The cost of sequence \(\sigma\) is given by \(C_\sigma=\sum_{t=1}^nC(i_t,i_{t+1})\). The goal is to find the sequence \({\sigma}^*\) that minimises \(C_{\sigma}\).
In the early days, given its success in solving Linear Programming (LP) problems, there was a lot of optimism that problems like the TSP could be solved efficiently by modifying the Simplex Algorithm. In particular Dantzig, Fulkerson and Johnson [6] formulated an approximate LP and solved a 49 city tour by adding extra constraints and re-optimising until the problem was solved. Computer Scientists formalised the notion of efficient (polynomial time) algorithms. The initial optimism was dealt a crushing blow by the seminal work of Cook [5], Levin [18] and Karp [14]. In particular, the theory of NP-completeness implies that there is a large class of (NP-hard) problems such that solving any one of them in polynomial time would lead to the efficient solution to all of them. Given that no one has found an efficient algorithm for any of these problems, one concludes that there likely isn’t one.
In reaction to this state of affairs, research on algorithms has branched in several directions. Some researchers have chosen to devise empirically efficient algorithms that have been able to solve enormous problems with many thousands of cities. (There is of course no guarantee for the worst-case time of such algorithms.) See the book by Applegate, Bixby, Chvátal and Cook, [1] some of the foremost researchers on these lines. A few people have studied special cases of the TSP, where assumptions about the cost matrix \(C\) lead to problems that are solvable in polynomial time. See for example the survey by Burkard, Deineko, van Dal, van der Veen and Woeginger [4]. Most of the effort has been spent on finding approximation algorithms that run in polynomial time and find solutions with a cost that is provably no more than some factor times the minimum. Finally, pioneered by Karp [15] researchers have constructed algorithms that work well with high probability (w.h.p.) and construct solutions that have cost within a factor \(1+o(1)\) of the minimum, as the number of cities \(n\to\infty\). This will be the subject of the remainder of this article.
There are two natural scenarios for considering random instances.
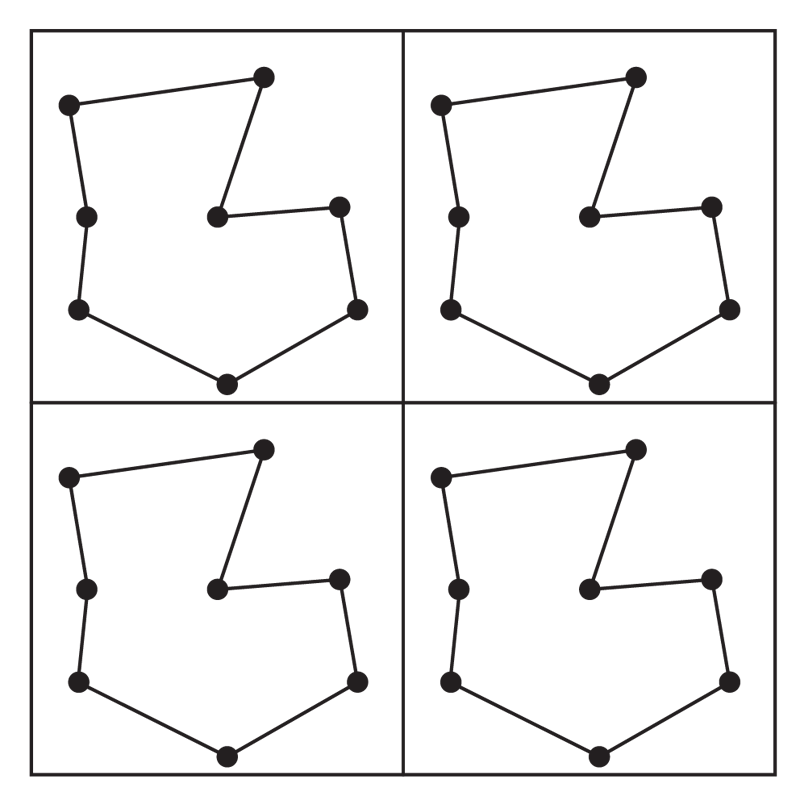
Figure 1(a)
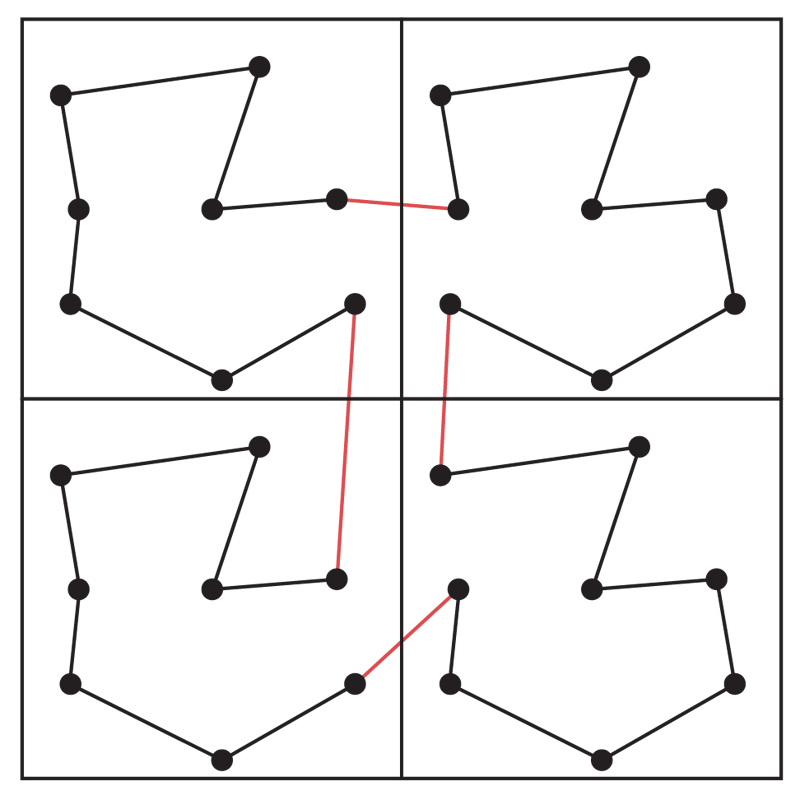
Figure 1(b)
2. Euclidean Problems
Here we assume that \(X={X_1,X_2,\ldots,X_n}\) is a set of \(n\) independent uniform selections from the unit square \([0,1]^2\) (more generally \([0,1]^d\)). The costs are given by \(C(i,j)=|X_i-X_j|\). Beardwood, Halton and Hammersley [2] proved that w.h.p. the cost of the solution to the associated TSP is asymptotic to \(\beta_{TSP}n^{1/2}\) for some constant \(\beta_{TSP}>0\) whose exact value is still unknown after more than 60 years. Karp’s idea is to partition \([0,1]^2\) into \(n/\log n\) subsquares of side \((\log n/n)^{1/2}\) and solve the \(n/\log n\) sub-problems using Dynamic Programming. See Figure 1(a). Then patch the subcycles into a tour as in Figure 1(b). Karp argued that the error could be bounded by a constant times the length of the boundaries of the subsquares. This is of order \(O((n/\log n)^{1/2})\) which w.h.p. is small compared the optimal tour length, given [2].
In the worst-case it takes \(n^{O(n^{1/2})}\) time to solve the Eucliden TSP exactly. Frieze and Pegden [9] showed that using the LP relaxation of [6] in a branch and bound algorithm is ineffective w.h.p. They showed that w.h.p. the algorithm needs to explore \(e^{\Omega(n/\log^6n)}\) sub-problems. In a follow up paper, Pegden and Sevekari [19] showed that branch and bound algorithm remains ineffective, even if one adds comb inequalities to the LP relaxation.
3. Independent Case
In this case we assume that the entries of the matrix C are independent random variables. This is unrealistic as a model for Euclidean problems, but has some relevance to some computational problems that can be transformed into TSP’s. There are a variety of scheduling problems of this kind.
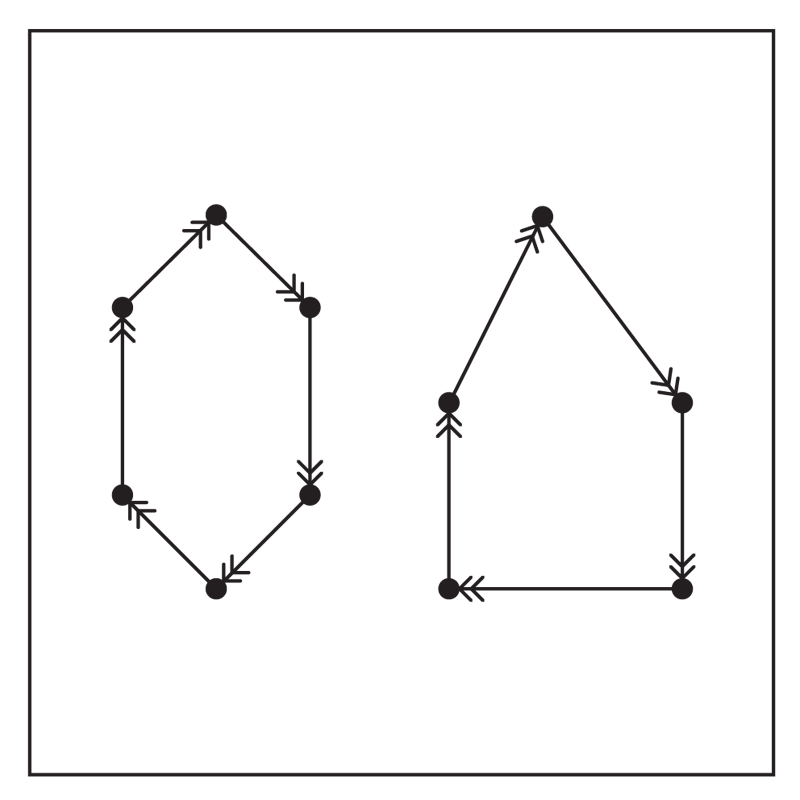
Figure 2(a)
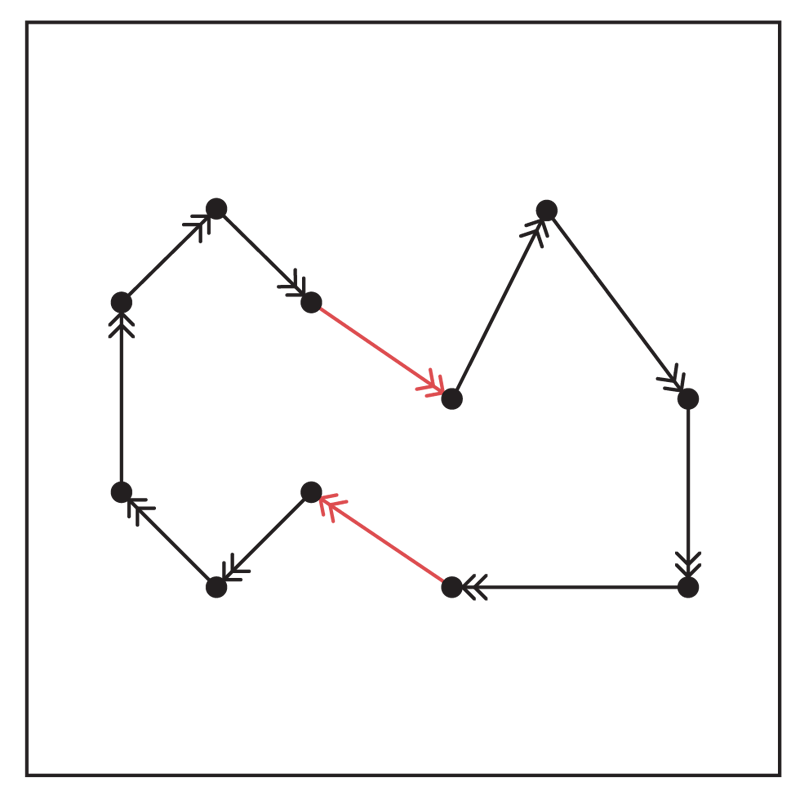
Figure 2(b)
3.1. Asymmetric Case
The first paper in this area was by Karp [16]. He assumes that the costs \(C(i,j)\) are independent uniform \([0,1]\) random variables. The \(Assignment Problem\) (AP) can be formulated as finding a minimum cost partition of the complete digraph \(\vec K_n\) into vertex disjoint directed cycles. As such it is always true that \(v(TSP)\geq v(AP)\) where \(v(\bullet)\) indicates the minimum cost. Karp’s patching algorithm proceeds as follows. Solve AP. This can be done in \(O(n^3)\) time. He argues that the optimum solution to AP corresponds to a random permutation of \([n]\) and so the optimal partition has \(O(\log n)\) cycles. His algorithm proceeds by merging cycles as in Figure 2.
This is done one by one until what is left is a tour. He argued that w.h.p. the total increased cost due to patching is \(o(1)\) w.h.p. Karp and Steele [17] gave a simplified analysis of the patching algorithm resulting in an improvement in the error bound to \(O(n^{-1/2})\). Dyer and Frieze [7] and Frieze and Sorkin [12] added a pre-processing phase to merging so that we can now say that w.h.p.
\[
v(TSP)=v(AP)+O(\frac{\log^2n}{n})\sim \frac{\pi^2}{6}.
\]
Our interest in improving on the error bound comes from trying to estimate the efficiency of using AP as a lower bound for use in a branch and bound algorithm for solving the asymmetric TSP.
We remark that if instead of using uniform \([0,1]\) costs, we generate them uniformly from \(0,1,\ldots,L=o(n)\) then \(v(AP)=c(TSP)\) w.h.p. This is the main result of Frieze, Karp and Reed [10].
As one final note on this topic, Frieze and Michaeli [11] consider replacing \(\vec K_n\) by a small random perturbation of an arbitrary dense digraph i.e. one with minimum in- and out-degree \(cn\) for some constant \(c>0\). (By a perturbation we mean the addition of \(o(n^2)\) random edges. A model introduced some time ago by Bohman, Frieze and Martin [3].) The resulting digraph is given random costs and we show that w.h.p. \(v(TSP)\sim v(AP)\). This somewhat more difficult, since we can no longer use uniformity to state that AP has \(O(\log n)\) cycles.
3.2. Symmetric Case
Here we assume that \(C(i,j)=C(j,i)\) for \(1\leq i,j\leq n\). It is natural to replace the AP by the problem of finding a minimum cost 2-factor of \(K_n\). A 2-factor is just a partition of \([n]\) into vertex disjoint cycles. This is again solvable in polynomial time, but we have less control over the number of cycles in the optimum solution. A random 2-factor will have \(O(\log n)\) cycles w.h.p., but ridiculous as it may seem we can only bound the number of cycles in the optimal 2-factor by \(O(n/\log n)\). Nevertheless, Frieze [8] showed that w.h.p. \(v(TSP)=v(2-FAC)+o(1)\) via the use of a hybrid greedy plus Hamilton cycle algorithm.
4. Conclusion
The TSP continues to be a subject of research. It is a test bed for ideas in Combinatorial Optimization. From the probabilistic point of view, determining the efficiency of branch and bound in the independent asymmetric model seems to be the most interesting problem. Perhaps also, gaining an understanding of the cycle structure of optimal 2-factors in the independent symmetric model.
References
[1] D. L. Applegate, R. E. Bixby, V. Chvátal and W. J. Cook, The Traveling Salesman Problem: A Computational Study, Princeton University Press, 2007.
[2] J. Beardwood, J. H. Halton and J. M. Hammersley, The shortest path through many points, Mathematical Proceedings of the Cambridge Philosophical Society 55 (1959) 299-327.
[3] T. Bohman, A.M. Frieze and R. Martin, How many random edges make a dense graph Hamiltonian?, Random Structures and Algorithms 22 (2003) 33-42.
[4] R.E. Burkard, V. G. Deineko, R. van Dal, J. van der Veen and G. Woeginger, Well-Solvable Special Cases of the Traveling Salesman Problem: A Survey, SIAM Review 40 (1998) 87-143.
[5] S. A. Cook, The complexity of theorem proving procedures. Proceedings, Third Annual ACM Symposium on the Theory of Computing, ACM, New York (1971) 151–158.
[6] G.B. Dantzig, R. Fulkerson and S. Johnson, Solution of a large scale Traveling-Salesman problem, Journal of the Operations Research Society of America 2 (1954) 393-410.
[7] M.E. Dyer and A.M. Frieze, On patching algorithms for random asymmetric travelling salesman problems, Mathematical Programming 46 (1990) 361-378.
[8] A.M. Frieze, On random symmetric travelling salesman problems, Mathematics of Operations Research 29 (2004) 878-890.
[9] A.M. Frieze and W. Pegden, Separating subadditive Euclidean functionals, Random Structures and Algorithms 51 (2017) 375-403.
[10] A.M. Frieze, R.M. Karp and B. Reed, When is the Assignment Bound Tight for the Asymmetric Traveling-Salesman Problem? SIAM Journal on Computing 24 (1995) 484-493.
[11] A.M. Frieze and P. Michaeli, Karp’s patching algorithm on random perturbations of dense digraphs.
[12] A.M. Frieze and G. Sorkin, The probabilistic relationship between the assignment and asymmetric traveling salesman problems, SIAM Journal on Computing 36 (2007) 1435-1452.
[13] G. Gutin and A.P. Punnen, The Traveling Salesman Problem and Its Variations, Kluwer Academic Publishers, 2002.
[14] R.M. Karp, Reducibility among combinatorial problems, in Miller, Raymond E.; Thatcher, James W. (eds.). Complexity of Computer Computations. Plenum Press, (1972) 85-103.
[15] R.M. Karp, Probabilistic Analysis of Partitioning Algorithms for the Traveling-Salesman Problem in the Plane, Mathematics of Operations Research 2 (1977) 209-224.
[16] R.M. Karp, A patching algorithm for the non-symmetric traveling salesman problem, SIAM Journal on Computing 8 (1979) 561—573.
[17] R.M. Karp and J.M. Steele, Probabilistic analysis of heuristics, in The traveling salesman problem: a guided tour of combinatorial optimization, E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan and D.B. Shmoys Eds. (1985) 181-206.
[18] L. Levin, A survey of Russian approaches to perebor (brute-force searches) algorithms, Annals of the History of Computing. 6 (1973) 384–400.
[19] W. Pegden and A. Sevekari, Comb inequalities for typical Euclidean TSP instances.
[20] A. H. G. Rinnooy Kan, D. B. Shmoys, J. K. Lenstra, E. L. Lawler, Traveling Salesman Problem – A Guided Tour of Combinatorial Optimization, Wiley and Sons, 1991.
